失敗と冪乗則 １

冪乗則に準じる失敗

失敗。かなり昔のことであるが、ある機会にこのテーマについて論じることがあり、それから深く考えるようになった。やがて私は畑中先生の「失敗学」なる学問があることを知り、さらに興味を持った。そしてはいわゆる「ハインリッヒの法則」なるものに惹かれていたのだのだが、それが本書で論じている揺らぎや冪乗則に関係することなど思いもしなかった。私はただ念のためにこの法則をここにお示ししよう。
■ハインリッヒの法則とは！？

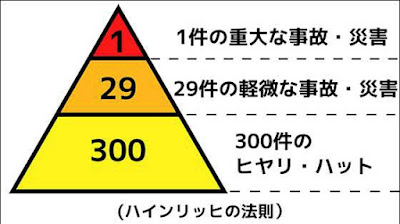
この図はアナザー茂さんという方のサイト（【統計学】失敗を未然に回避するヒヤリ・ハットの法則！ 魔法の比率「1：29：300」2014年8月20日 17:00）から借用した。その解説によると、ハインリッヒの法則は、ハーバート・ウィリアム・ハインリッヒという保険会社の調査部の方が、なんと1928年も昔の論文で唱えた法則である。実際にそれが発表された著書には彼自身の手書きのピラミッドの図がある。
「ハインリッヒは5,000件以上に及ぶ労働災害を調べ、1件の重大事故の背景には、29件の軽い『事故・災害』が起きており、さらに事故には至らなかったものの、一歩間違えば大惨事になっていた『ヒヤリ・ハット』する事例が300件潜んでいるという法則性を示したものである。ハインリッヒの法則は、その内容から別名『ヒヤリハットの法則』とも呼ばれ、『1：29：300』という確率はその後の災害防止の指標として広く知られるところとなった。」

例えば、ある工場で1件の重大事故が発生した場合を考えよう。おそらくその工場では、そこまでには至らなかった事故が、過去に29件発生していたはずだ。そしてそこにまでは繋がらなかったより軽微な事情は300件起きていたはずである。

私がなぜそこまでこの件にひかれたかはわからないが、おそらく本当に偶発的としか思えない事件の背後にある種の法則があることを知らされたからである。皆さんお分かりの通り、この件はまさに冪乗則である。しかし1920年当時にそのような概念は一般に普及していなかったはずだ。そしてハインリッヒはそれを直感的に認識したというわけである。

私は病院勤務の経験が長いが、病院とはまさに失敗や災害、有害事象が起きやすい環境である。私自身も特に米国でのレジデントの最中に、何度も肝を冷やす体験をした。「あの時もしあれが起きていたら、今の自分はこうしていることは出来なかった」ということは何度もあるのである。ただしそれは実際に起きなかったわけだが、他方ではなぜこんなことがいきなり起きたんだ！ということもある。顧客にかかわる事象などはその典型例かもしれない。「万が一のことがあるかもしれない」と頭に浮かぶ人はたくさんいる。しかし実際の深刻な事象は予想外のところから起きてくることが多い。このように書くと私は本当はハインリッヒの法則に当てはまらないことばかり体験している可能性がある。30例の中からの一件は「きたか！」という形で受け入れていて、いざというときの意外性はあまりないのかもしれない。しかしそれ以外の、全くノーマークのところから起きてくることには、まさに300のうちからいきなりポンと起きてくるということが考えられる。あのピラミッドは本当なのだろうか？　ちょっと批判的に考えていきたい。