1920年当時にそのような概念は唱えられておらず、もちろんハインリッヒも知りようもなかった。しかしハインリッヒはこのべき乗則に近い法則を直感的に認識したということではないだろうか？ 事実ハインリッヒの法則について考えると、ひょっとしたらこれはべき乗則についての洞察の一歩手前の状態ではないかとも思えるのだ。なぜなら失敗は、べき乗則に従うような出来事、つまり地震や株価や戦争と似た性質を有する。つまり大きなものほど稀に起きる、という性質である。そして失敗もその典型例だと考えてもおかしくない。
そこで上に見たピラミッド型の図を、べき乗則に従うものとして描き換えるとどうなるのだろうか？ まず以前に●章で示したロングテールの図は以下のとおりである。ハインリッヒの図は一番大きいものを頂上に乗せて、より小さいものをその下に配置している。それは理屈から言えば、ロングテールの図を盾にして左右張り合わせたものに事実上一致することになる。
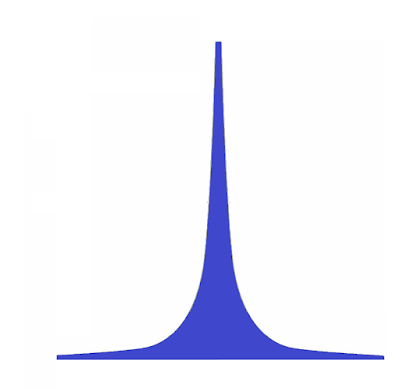
これを二枚用意し、片方を反転させてつなぎ合わせ、90度回転させると以下のようになる。実はハインリッヒが描こうとしていたのはこれではなかったかという疑いが生じる。
ちなみに「ハインリッヒの法則」と「べき乗則」という二つのキーワードでネットで検索してみよう。両方のつながりは結構示唆されているが、「ハインリッヒの法則は結局はべき乗則である」と言い
しかしいろいろ考えた末、私はハインリッヒ則とべき乗則は類似のものと考えるに至った。
