失敗と冪乗則 ３

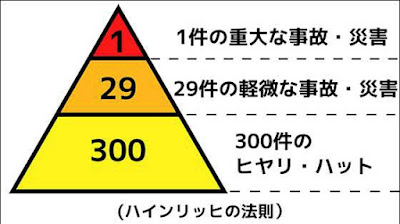
ところでハインリッヒは実際にどう考えていたのだろう。ここに掲げたのは彼の著書に示されている図であり、その説明である。

彼はすべての事故がたとえば330回起きると仮定する。そしてそのうち300回では、人は外傷を負わないとする。そして29回は軽症の外傷を負い、1回は重症の外傷を負うとする。そして重症の外傷は、この330回のうちいつ生じるかわからないとし、また教訓 moral として、「とにかくインシデントを防ぐべし。さらば外傷はおのずと回避される」とする。

このハインリッヒの記載から伺えるのは、労災には理由があり、それは大小を問わず、事故であり、それが存在する限りは外傷は生じるべくして生じるという考え方である。このスタンスは冪乗則と似ているようで異なっていると考えるべきだろう。それは大事故には理由、ないしは原因があるとするところだ。ただしその原因とは原因ともいえないようなインシデントであり、そのどれが外傷を伴った労災に発展するかはわからないとも言っているようだ。ん？何か堂々巡りをしていないだろうか。よくわかっていなくてウロウロしている証拠だ。

結局私たちは次の二つの立場の違いを扱っているのだ。

１． あらゆるインシデント(正常とはいえない事態)が、重大事故に繋がる可能性を有している。(ハインリッヒ)

２． あらゆる揺らぎが、激震に繋がる可能性を有している。(冪乗則)

こうやって書いてみると同じことのようだ。１．は「ではインシデントを完全に防ぐことは出来るのか?」と聞きたくなるが、実はハインリッヒ自体が、そんなことは無理だといっているらしい。(今度ゆっくり原典に当たってみよう。)だからその意味では彼の立場は 2. に近いことにある。また２. については、では揺らぎがないところには激震もおきないのか、ということになるが、そもそもプレートの境目から遠く離れた、プレートの中央付近なら、地震は基本的に起きないだろう。たとえばこの図からは北アメリカの中央付近にはほとんど地震が起きないことになる。

北米大陸は真っ白な部分が多いが、そこは私が17年間暮らしたカンザス州のトピーカも含まれる。そしてそこでは地面の揺れを感じたことが、17年間の間一度もなかった。これはちょうど稼動していない工場ではインシデントが起こりようがないということになる。人は1．の場合は重大事故の「原因」は明確であり、それはインシデントであり、それにだけ注意して仕事をすればいい、というだろう。確かにそうかもしれない。でもそれと同じことを 2. では言いにくい。地震がまったく起きないところにいかない限り、地震の多発地帯では頻発する地面のゆれは、いくら努力しても止められるものではない。でもたとえば工場での生産を100パーセントロボットに任せるという奥の手を使ったら、インシデントをゼロに近くできるかもしれないし、将来どのようなテクノロジーが開発され、地殻の微少のゆがみを正すべく規則正しい振動を地面に与える、などの技術が出来るかもしれない (まったくの想像でテキトーに書いているが)。つまりは１.と２.はあまり変わらないということを言いたいのだ。ということで私なりの結論としては、ハインリッヒの法則は、冪乗則として洗練されてはいないものの、似たような発想によるものであり、彼の考えたピラミッドは結局はロングテールの左右張り合わせのことだ、ということである。二等辺三角形の図は単純化しすぎで誤解を招きやすいだろう。

失敗と冪乗則 ２

ハインリッヒの法則について考えているうちに、これと冪乗則とは微妙に違うような気がしてきた。ひょっとしたら、ハインリッヒの思考は、冪乗則についての洞察の一歩手前の状態ではないかと思えるのだ。だって失敗は、いかにも冪乗則に従いそうな感じではないか?　地震も株の高騰や暴落も戦争も、皆冪乗則に従う。失敗だって、その典型例だと考えられてもおかしくない。

ハインリッヒの法則とは何かを読むと、大事故にはそれなりのきっかけがあるということを言っているようだ。大きな事故は、それを起こしかねない30の小さな事故から発展する、と言っている気がする。しかし地震はいかにも起きそうな30カ所の中から選ばれて起きるだろうか？おそらくそうではない。無数の地震発生地の中から、何らきっかけもなくドーンと起きるのだ。それとは異なり、工場における失敗はその兆候を知ることが出来、もう少し予測不可能ということになるのだろうか。

例を考えてみる。最近起きた、新幹線の台車が破断寸前まで行ったという事件。これは予兆があっただろう。しっかりとした点検をしていれば防げたはずだ。問題があそこまで進む予備軍がほかにも29 (実は1対29の比率にこだわる必要は全くないのだが) くらいの問題があったと言えるかもしれない。そしてそれらの29のそれぞれが、10くらいのマイナーな問題を見過ごすことにより生まれた、と考えるのだろう。とすると事件が起きる背景はかなりはっきりし、それは結局は理論的な手法をたどれば防げる、と考えるべきなのだろう。しかしそうだろうか。おそらくそうではない。大事故は29の予備軍から起きる、という見方そのものが怪しい。

殺人事件を例にとろう。多くの殺人には何らかの予兆があるだろう。AがBに殺意を抱く。そしてある日凶行に及ぶ。これは確かに大事件だ。しかしAを知っている人は大抵言うのだ。「Aさんはごく普通の人でしたよ。挨拶もするし。」そう。「普段から何をする人かわからず物騒でした。」というケースはむしろ少ないのだ。Aは殺人者予備軍、つまりいつ爆発するかわからない30人、というのとは違うプロフィールを持っていることがおおい。彼はむしろノーマークなのだ。ちょうど大地震が起きた時と場所が大抵ノーマークであったのと同じように。

ということは私のハインリッヒの法則の理解の仕方が間違っていたのか。例のピラミッドの絵が紛らわしいという事はないか。あの絵が下の段の中から一つが選ばれる、ということを意味しているのと誤解されるのではないか。ただ数を表しているにすぎないのだろうか。もしあれが冪乗則に従うとしたら、ピラミッドとは似ても似つかない形の絵を描かなくてはならないだろう。数日前のロングテールの表を思い出そう。あれをピラミッド型に描き変えるとどうなるのか。

これがその図であるが、これは数日前に出てきたロングテールの図を片方を反転させてつなぎ合わせたものだ。昨日のハインリッヒの図は逆三角形だったが、実はハインリッヒが描こうとしていたのはこれではなかったか。

ここで気になってネットで「ハインリッヒの法則」と「冪乗則」を検索していた。両方のつながりは結構示唆されているが、「ハインリッヒの法則って、結局は『なんちゃって冪乗則』じゃない?」と言い切っている文章には出あわなかった。でもそう考える人がいてもおかしくないだろう。

失敗と冪乗則 １

冪乗則に準じる失敗

失敗。かなり昔のことであるが、ある機会にこのテーマについて論じることがあり、それから深く考えるようになった。やがて私は畑中先生の「失敗学」なる学問があることを知り、さらに興味を持った。そしてはいわゆる「ハインリッヒの法則」なるものに惹かれていたのだのだが、それが本書で論じている揺らぎや冪乗則に関係することなど思いもしなかった。私はただ念のためにこの法則をここにお示ししよう。
■ハインリッヒの法則とは！？

この図はアナザー茂さんという方のサイト（【統計学】失敗を未然に回避するヒヤリ・ハットの法則！ 魔法の比率「1：29：300」2014年8月20日 17:00）から借用した。その解説によると、ハインリッヒの法則は、ハーバート・ウィリアム・ハインリッヒという保険会社の調査部の方が、なんと1928年も昔の論文で唱えた法則である。実際にそれが発表された著書には彼自身の手書きのピラミッドの図がある。
「ハインリッヒは5,000件以上に及ぶ労働災害を調べ、1件の重大事故の背景には、29件の軽い『事故・災害』が起きており、さらに事故には至らなかったものの、一歩間違えば大惨事になっていた『ヒヤリ・ハット』する事例が300件潜んでいるという法則性を示したものである。ハインリッヒの法則は、その内容から別名『ヒヤリハットの法則』とも呼ばれ、『1：29：300』という確率はその後の災害防止の指標として広く知られるところとなった。」

例えば、ある工場で1件の重大事故が発生した場合を考えよう。おそらくその工場では、そこまでには至らなかった事故が、過去に29件発生していたはずだ。そしてそこにまでは繋がらなかったより軽微な事情は300件起きていたはずである。

私がなぜそこまでこの件にひかれたかはわからないが、おそらく本当に偶発的としか思えない事件の背後にある種の法則があることを知らされたからである。皆さんお分かりの通り、この件はまさに冪乗則である。しかし1920年当時にそのような概念は一般に普及していなかったはずだ。そしてハインリッヒはそれを直感的に認識したというわけである。

私は病院勤務の経験が長いが、病院とはまさに失敗や災害、有害事象が起きやすい環境である。私自身も特に米国でのレジデントの最中に、何度も肝を冷やす体験をした。「あの時もしあれが起きていたら、今の自分はこうしていることは出来なかった」ということは何度もあるのである。ただしそれは実際に起きなかったわけだが、他方ではなぜこんなことがいきなり起きたんだ！ということもある。顧客にかかわる事象などはその典型例かもしれない。「万が一のことがあるかもしれない」と頭に浮かぶ人はたくさんいる。しかし実際の深刻な事象は予想外のところから起きてくることが多い。このように書くと私は本当はハインリッヒの法則に当てはまらないことばかり体験している可能性がある。30例の中からの一件は「きたか！」という形で受け入れていて、いざというときの意外性はあまりないのかもしれない。しかしそれ以外の、全くノーマークのところから起きてくることには、まさに300のうちからいきなりポンと起きてくるということが考えられる。あのピラミッドは本当なのだろうか？　ちょっと批判的に考えていきたい。

人の行動と臨界状況 4

パラノイアの延長としての戦争

　さてパラノイアの帰結としての最大級のものは何か、ということに関しては、先ほどは 30人が巻き込まれた最近の火災を例に挙げたが、さらに上の段階の出来事が幾らでも考えられる。そのひとつは戦争である。そしてこの問題についても見事な議論を行っているのが、すでに述べたアルハート・ラズロ=バラバシの「バースト!　人間行動を支配するパターン」（青木薫訳、NHK出版、2012年）である。この不思議な本では、現代社会において人間が起こす行動の複雑さ、乱雑さがいかに冪乗則にしたがったものかという話の一方では、16世紀にハンガリーで起こった十字軍の反乱事件が交互に、刻一刻と描かれている。実際に起きた歴史的事件がいかにさまざまな偶然により衝き動かされていったかについて、いくつもの実例があげられているわけだ。
　その本の第11章は、「死にいたる争いと冪法則」と題して、ルイス・フライ・リチャードソンという学者が、戦争がどのようにして起きるかについての法則を探し求めた話がある。いろいろな仮説があげられたそうだ。「経済力に大きな差がある国同士の方が交戦する可能性が大きい」「共通の言語を持つ集団同士の方が争いになりにくい」「軍拡競争はいずれ交戦が起こることの前ぶれである」などなどであったが、結局データを見る限り、戦争を引き起こすのは、全く偶発的な現象であることが分かったという。そしてそこにはまさしく冪乗則が見つけられたのだ。そしてその中の最大級の、数千万の命を奪った、しかし数にしてわずか二つの戦争（いうまでもなく第一次、第二次世界大戦）を筆頭に、少し規模の小さい６つの戦争が続き、そのあとは延々と小規模の戦争が続いていく、というわけである。　それにしても最大級の戦争の下には、最大級の揺らぎが生じていたことを想像するのは空恐ろしいことだ。皆さんもおそらくご存知のキューバ危機。1962年10月から11月にかけてキューバに核ミサイル基地の建設が明らかになったことからアメリカ合衆国がカリブ海で海上封鎖を実施し、アメリカとソビエト連邦とが対立して緊張が高まり、全面核戦争寸前まで達した危機的な状況のことである（Wiki）。最終的には当時のアメリカ大統領ケネディとソ連の首相フルシチョフの間でのやり取りがあり、一触即発の危機が解除されたというが、結局そちらの方に揺らいだからこそ戦争は起きなかった。しかしもし間違った方に揺らいでいたら・・・・。真珠湾のようなことになっていたのだろうか。本当は巧妙な駆け引きがそこで行われていたという説を信じたい人もいるだろう。しかし私はそれをあまり信じない。Buchanan の”Ubiquity” の冒頭には、第一次大戦が1914年6月28日の午前11時に、ある車の運転手が犯したちょっとした間違いが第一次大戦の勃発につながった様子が描かれている。私はこちらの方を信じるし、それは次に述べる「失敗」の法則にもつながる。失敗もまた、人間の冪乗則にしたがう行動の一つの典型である。

人の行動と臨界状況 ３

さて、冪乗則は一応なんとなくわかったことにして、これが心理の世界にどのように絡んでくるか、である。これが本来の関心の的だった。ひとつの例として私が考えるのはパラノイアである。私は被害妄想は人間の心理の基本中の基本と考える。どんなに楽天的な人でも被害的になりうる。それは人間の思考の構造がそのようにできているからだ。そしてそれは極めてまれにではあるが、大きな事件に発展する。そしてそれが大きくニュースにとりあげられるのだ。他方では些細なパラノイアは常におきていると考えていい。人間の心は、他者の言葉を普通に受けとることと、裏読みをするとの間を揺らいでいるのである。

まずは大きい事件からだ。ごく最近起きたニュースにヒントを得ている。ある人間が誰かに恨みを持ち、攻撃を仕掛ける。昔の話で言えば忠臣蔵のようなものだ。四十数人の人間を巻き込んで刃傷沙汰が起きた。そしてごく最近ではある恨みを持った人の犯行により、三十数人の尊い命が奪われた。これらがおそらく最大級のレベルのパラノイアの例とするならば、それより小規模の例はずっと頻繁に起きている可能性がある。同僚が自分にことさら悪意を持っている気がして思わずきつい言葉を投げかけてしまう。そのやり取りが周囲に緊張感を与え、周囲はハラハラしながらそれを眺める、といった程度。顕在化した、ちょっとした衝突や口論のレベルで表出するパラノイアはどのような集団でも年に一度や二度は起きるかもしれない。

そしてそれよりさらに多いのが、具体的な発言や行動に移されることなく、「あいつ、何やネン！」という気持ちを抱くような状況である。これなど人が集まって何かをする際には起きないことのほうが少ないのではないか。人がグループを形成するところでは、必ずといっていいほど内輪もめが生じる。そしてその最小単位といえば、それこそ人と人とが交わすコミュニケーションにそれは見られる。人は他人の言葉を額面どおりに取らずに裏読みすると、当てこすり、皮肉、中傷など、こちらに対する攻撃の意図をそこに読み取るのだ。

人の行動と臨界状況 ２

ただしここで大事なことがある。臨界状況はでも冪乗則を形成するとは限らないという事だ。だって麦茶を飲む人は結局は、ごくまれに100杯飲む人がいて、さらにごくまれに1000杯飲む人もいて、という事にはならないからだ。これってどう考えればいいんだろう。

先ほどの競売の例の場合は、落札金額について大体冪乗則が期待できそうだ。ヤフオクで扱われる膨大な小物は少額であり、高価な落札金額で取引されるものほど数としては少なくなりそうだ。ただし個人の売買の落札価格となるとかなり違うだろう。高額といってもたかが知れているであろうからだ。でもいつもは数百円の規模でヤフオクで取引をしている人も、何年かに一度は百万単位の取引をするかもしれない。ちょっとは冪乗則に従いそうだ。しかしたとえば上の麦茶の例だ。人は「ごくたまに、絶対100杯飲む」という風にはならない。おそらくこちらの方はポアソン分布に近いだろう。真ん中に頻度の高い山が出来る、あれだ。人間の身長、体重、知能などはことごとくこれである。ごくまれにIQが1000を超える人などいない。ごくまれに身長が10メートルの人がいるという話も聞いたことはないのである。こちらの方はちゃんと「平均値」を求めることが出来る。ロングテールなどありえない。（世界の人口の8割は、身長が10センチ未満である?）これはどうしてだろうか?生命現象のせいだろうか?　生命活動を営むという条件が、そのサイズに圧倒的な制限を加えている?　でも地球上の生命体のサイズを平均したら、莫大な数を誇るウイルスや細菌のそれに近くなる、というのはかなり冪級数的だ。もちろん地球サイズの生き物はどんなにまれにも存在しないという意味では上の方はかなり制限されることになるが。何がポワソン分布に従い、何が冪則に従うか。基本的なことが分からなくなってきたぞ。

人間がメールを打つ回数には冪乗則が成り立つ、とバラバシの「バースト」には書いてあった。でも考えてみれば、人はごくまれに一日に5000回メールを打つ、なんてことはあり得ない。平均してゼロ、という事もない。なのにあれも冪乗則に従う、という事にしていた。という事はポワソン分布に従う者のごく一部の領域について冪乗則が成り立つ、という事だろうか。おそらくそうなるだろうが（後で確かめる）、一つ分からなくなることがある。これまでの考察から、冪乗則は最小単位、例えば砂粒とか水の分子から考えたから成り立つという気がする。始まりは微小単位でなくてはならない。ところが途中だけ冪乗則、というのであれば、この最小単位を考えることが出来なくなる。これが育っていく途中から急に冪乗則というのであれば、少し別の考え方をしなくてはならないのだろうか。とにかく人間の行動についてはポワソン分布と冪乗則が混淆しているという理由がわかるようでわからない。

そこでもう一つの資料をネットで拾った。これはAOL(アメリカオンライン)の利用者がいくつのサイトを見たかという情報を基にしたものだが、ほんの数サイトが2000回以上の訪問を受けている一方では、ほとんどのサイト（約70000)が一度しか訪問を受けていないという関係を表している。さてこの線の直線部分が冪乗則を表しているのはいいとして、下のあたりが気になる。直線が崩れているからだ。これを見ると2500のサイトは一人しか、1700のサイトは二人しか、1400のサイトは3人しか訪れなかったということを意味しているようだ。もしここに厳密に冪乗則が当てはまるならば、5000のサイトには0.5人しか、100000のサイトには0.2人しか・・・・みたいになるのだろうか？しかし人の単位は一人以上だからこれはあり得ないし、サイトの数だってさすがに100億などありえない。1000億のサイトに0.001人しか訪問していない、等。だから最小単位の肌理の細かさ（粗さ？）によって、どこまで冪乗則が当てはまるかが違ってくる、と考えればよいのだ。

人の行動と臨界状況 １

冪乗則に関する考察の続きで、臨界状況について考えている。こんな状況を考えた。セリである美術品が出る。100万円では安い、ぜひ手に入れたいツボだ。ところが競争相手が出てきて、値を吊り上げていく。120万と言い出した。「120万か、まあもうちょっと押そう」と140万と希望値を伝える。「これでギリギリだ」と思いながら。すると相手は150万!　とさらに吊り上げる。あなたの中で何かがぷつんと切れる。「こりゃなしだな!」と引き下がる。あれほどよさげに見えた、深みと光沢の加減が何とも言えない青磁のツボ（まったくテキトー）である。でも140万だったら欲しくて、150万だったらいらないって、どういう事だろうか。差額は10万である。その10万で次に出てきたどうでもいいような骨董品を、「まあ。安い買い物だな」とか言いながら買っているのである。これって、なんか臨界に関係するような気がする。消費行動において起きているのは、この140万なら買うが150万なら買わないという、ある意味ではランダム性を帯び、理屈に合わない行動であり、実はそれが臨界状況を表しているのだ。人はこれを揺らぎの一種と捉えるかもしれない。丁度氷の枝の近くをフラフラ通った水の分子が、そこに付着しようかしまいか迷うという状況だ。揺らぎとは、まさにこの付こうか付くまいか、買おうか買うまいかといういい加減さであり、この種のゆらぎを含んだ行動は、たとえば株の取引などで顕著になるのではないだろうか。ちょっとした根の動きで行う売り買いは、おそらくかなりランダム性に富んでいて、それは微妙な状況であればあるほどサイコロころがしに近くなるのだろう。すると臨界状況を作り出しているのは、このサイコロころがしではないか、という事になる。まあ恣意性、といってもいいだろう。すると基本単位が恣意の積み重ねにより成り立つような人間の行動は、ことごとく臨界状況を生み出すのではないか。というよりかそこまで行ってやっと人間の行動の動きは止まるという感じだろうか。するとこう問いたくなる。人間の行動の中で、臨界まで進まないものはいったいなんだろうか。私が好んで引用するウォーコップ・安永理論では、人間の行動は生きる行動と、死を回避する行動のせめぎあいである。伸び伸びと自由に行っている行動は、すぐどこかで限界に達する。暑い夏に外出先から帰る。冷蔵庫から麦茶を出してのどを潤す。どんなにのどが渇いて、最初の一杯が心地よくても、大体3杯目くらいにはきつくなってくるだろう。それでも3杯目を飲み干すかどうか、微妙な時にサイコロは振られる。ここは臨界状況となり、揺らぎが働く。

冪乗則と揺らぎ 6

冪乗則についてのいつ終わるともしれない話につきあっていただいている。でも残念ながら、私にはまだ全然わかっていない。というか、本来そんなに簡単にわかることなどできないという気になっている。ただ一つこんなことが言えるだろうか?　まずこの世の中はとんでもない複雑な世界である。そこにはそれぞれの運動にある種の最小単位を考えることが出来、それがさまざまなインターラクションを起こしながら、世界の動きを形成していく。世界が複雑で、そしてそこにエネルギー源があれば、それは常に動き、さまざまな現象を生み出す。そしてそれは基本的には「動的平衡」を保ちつつ変化していく。「動的平衡 dynamic equilibrium」とはWiki 様によれば、「互いに逆向きの過程が同じ速度で進行することにより、系全体としては時間変化せず平衡に達している状態」だという。まあ当たり前だけれど。日本ではこの概念は、福岡伸一先生のエッセイで有名だ。でも動的に平衡であるという事は、臨界が近いという事でもある。世の中が大体安定しているという事は、そこでの動きはゆっくりである程度はどこに向かっているかが予測可能な状態だという事だろう。たとえば常温での水は、気体になって行く分子と液体になる分子の両方向のバランスが取れている。つまり「動的平衡」だ。ところが水が冷えて徐々に氷になって行くという状態では、動的平衡が崩れ、臨界状態が進行していることになる。だからこそ氷が大きくなっていくという形での「変化」が生じるのだ。つまり変化が起きる時に一つの動的平衡からもう一つの動的平衡の間に繰り広げられるのが臨界状態であり、そこには大概冪乗則が出現する、という仕組みなのだ。そしてこの世は常に変化しており、だからこそ冪乗則は至る所に存在する ubiquitous というわけだ。何か不思議なようで当たり前な話。

水から氷のことを考えよう。最初に水の中の塵を核にし、小さな氷の結晶が出来上がる。するとそこに次の氷の粒がくっつき・・・・。そこからの仕組みはDLAで見たとおりだ。変化はあるきわめて微小な形で起き、そこから小さな粒、大きな粒が出来上がり、小さな粒は小さいなりに、大きな粒は大きいなりにスケールフリーで出来上がっていく。この様子は見てきた。

では人間の活動についてもどうしてこれが言えるのか。というより何が臨界状態なのだろう？　たとえば富はどうか。もし世の中の人間がすべて同一の富を有していたとする。商取引をして金の出し入れはしているから動的平衡は保たれている。もし富が変化していかないなら臨界は起きない。しかし実際の世の中では、貧乏な人は一生懸命お金を稼ごうとする。それぞれがある状態から別の状態に向かって動こうと企てている。これがいわば臨界状態を結果的に作り出しているという事だろう。丁度氷結する際に水の分子が一生懸命すでにできている氷の塊にくっついて、隙あらば氷として成長しようとしているのと同じように。あるいは地震の例では、マグマの流動という外的な影響により、地殻を形成する砂の粒がどれも隣りの粒とのずれによる力を緩和させようとしているという形で臨界状況を作っている。

あるいは株取引などは典型的ではないか。それぞれの投資家が少しでも利益を出そうとして、高くなったら売り、安くなったら買おうとする。だからそれぞれの投資家の存在はそれ自体が臨界状況を作り上げている。アルハート・ラズロ=バラバシの「バースト!　人間行動を支配するパターン」（青木薫訳、NHK出版、2012年）を読んでいると、人のメールや手紙を送るタイミングが冪乗則に従うという事が書いてあるが、メールを返す、手紙の返事を書くという事が冪乗則に従う時は、その人がかなりアップアップし、必死になって追い付こうとしている時に、臨界状態を表す「バースト」が現れる。この場合の臨界とはいっぱいいっぱいの状態であるということだろう。つまり自由意思で何かをのんびり行っている時は臨界は訪れず、やむにやまれずに何かを行っている時にこの臨界が現れる。となると臨界とは人間が必要に迫られて行動を起こすところには常にあらわれてもおかしくない。そして人間のその行動にとって、ちょうど氷や砂粒のかけらに相当するもの、それが揺らぎを構成しているという事だ。どうだろう。ちょっとまとまってきたかな。

冪乗則と揺らぎ 5

これで少しは落ち着いて考えられそうだ。なぜ物事に冪乗則が成り立つかを克明に追うことができる。そこで改めて考えよう。上から雪のように、分子がランダムに地面に降ってくる。地面に落ちた分子はほとんどそのままだろうが、中には降ってきた次の分子をくっつけて枝を伸ばしていく。さてここに冪乗則が成立するということはどういうことだろうか。例えば二倍の大きさに成長する確率はX分の一。このXに入る数字はおそらく状況により異なるのだろう。ここで大切なのは、小さい枝は小さいなりに、大きい枝は大きい枝なりに成長していくことだ。そしてその成長の仕方はスケールフリーということになる。どの大きさの枝に自分がなりきっても、大きく成り方のペースは同じに感じられるだろう。その成長の仕方は、どんなにズームインしても、ズームアウトをしても同じ。そういうことだ。なぜそうなるのか。自分が大きい枝なら、それだけ表面積が大きいから、より多くの分子がぶつかってきて、それをくっつけることができる。つまり最初にあった格差、不平等がより大きくなっていく。Rich gets richer というわけだ。ではその不平等の起源は何か。最初には最小単位の枝、つまり一粒の分子がバラバラに転がっているというところから出発する。最初の差は次の分子をいかにくっつけることができるかだ。そしてそれは完全に偶発的なことだろう。
思考実験を簡単にするために、地面には一面に一つの分子が敷き詰められているとする。分子が降ってくる確率をPとしよう。そして最初の一定の時間に格差が生まれるということにしよう。すると一つゲットする確率はP分の一、二つはP二乗分の一、3つはPの三乗分の一。これで最初の枝の大きさの格差が生まれた。何とか冪乗則に従っているようだ。そしてあとはそれぞれの枝が、同じことを繰り返すことになる。つまりそれぞれの枝でまた同じことが起きる。そしてその枝の中でもその小枝で冪乗則が成り立っていく…。まあいいか、これで分かったことにしよう。

結局何が知りたかったのか。それは冪乗則がどのような意味で人間の活動にも当てはまるかが知りたかったのだ。Bourke 氏のサイトでは、この法則が当てはまる例として、珊瑚の成長、稲妻の長さ、塵や煙の集積、ある種の結晶の成長などをあげているが、居酒屋を出て酔っ払いが歩く距離も例に出している。ほとんどの人が2，3歩で倒れるが、一部の人は10メートル歩き、さらにまれに100メートル歩く人がいる、等の例だ。半分冗談かもしれないが、これが人の資産とか、本やCDの売れ行きにも当てはまる。ということは一円ごとの富の集積、一冊ごとの本の売れ行きなどが、この分子の動きと同等ということになる。例えばたった一冊しか売れなかった本より、2冊売れた方が、それを目にしたほかの人が買うという可能性が高くなる、という風にして冪乗則が成り立つ。あるいはお金を1000円持っている人より、2000円持っている人の方が、より仕事を得てそれ以上にお金を稼ぐことができる、ということだろう。なぜだろうか？それはよくわからないが、そこにある種の偶発性が深く絡んでいることはわかる。世界中で一人しか持っていない本よりも、二冊持っている本の方が、たまたま人の目に触れて買ってもらえる確率が高くなる。それは本が面白いから、というのとはかなり異なった力学が働いている。

しかしここで私は思うのだ。作られたときにすでにヒット間違いなし、という曲はないだろうか？ビートルズの「イエスタデイ」は、ポール・マッカートニーが朝起きて夢に出てきたそのメロディーを口ずさんだ時に、すでにビリオンセラーになる運命にあったのではないか。それは偶発性だけだろうか？うーん、ナゾは続く。

冪乗則と揺らぎ ４

冪乗則のことが、まだ本当にはわかっていないので思考を続ける。これまでの考察からは、どうやら冪乗則にしたがうものにはある種の歴史が読み取れそうだということがわかるだろう。小さな砂粒大のかたまりのずれが、場合によっては連鎖反応を起こして巨大な地震につながる、という場合、明らかに時間の流れに即した動きが読み取れる。ただそのような爆発的な動きがあまり感じられないものもある。

ここに示した画像をご覧いただきたい。これは高熱で溶けた銅を冷やすと表面に広がっていく結晶だという。ちょうど雪の結晶が形成されるのと似ている。Witten and Sander’s game  というのが、この画像に示されるような現象をさすというのだが、これは「拡散律速凝集」Diffusion-limited aggregation　(略してDLA)と呼ばれるそうだ。最初にどこかに小さいチリなどを核として銅が固化すると、あとは近くの分子が次々とくっついていく。そしてこのような木の枝のような形が形成されていく。拡散律速、という意味は、銅の分子がまばらに、拡散された形でたまたまできかけた結晶にくっつくというやり方が律速段階になっている、あるいはスピードを制限しているということであり、要するにバタバタッと一気に起きるという形はとらないという意味だそうだ。これはコンピューターでも簡単にシミュレーションを行うことが出来る。

さてこのDLAも冪乗則にしたがった形成のされ方をするという。中央の最初の結晶が生まれた部分を拡大していくと、最初の枝分かれが生じていることがわかる。この写真を見る限り4つあるようだ。そしてそれぞれの枝がどんどん広がってできた様子がわかる。おそらく時間としてはかなりゆっくりで、最初の点からじわじわ広がっていくことが、コンピューターのシミュレーションからもわかる。さてここで何が冪乗則にしたがっているかと言えば、枝の大きさである。小さい枝は限りなく多く、そのサイズを大きくしていくと、数は減っていく。最後にはこの全体が一つの巨大な枝として出てくるわけだ。そしてその枝を大きさの順に並べると、ロングテールが出来上がる。さてこの場合の冪乗則はそこに巨大な連鎖反応と呼べるような出来事は起きていないようだ。ここに見られる大物は、最初に枝分かれをして、あとは途切れることなく枝を伸ばすことが出来たもの、ということになる。

このテーマに沿って調べていくうちに、Paul Bourke という人のサイト（DLA - Diffusion Limited Aggregation）に行き当たったが、これが素晴らしい。そこに私が一番知りたいようなモデルが出ていた。 

この図のどこがすごいのだろうか。これは上から降ってきた点が下に積もっていくという形で枝が成長していく様子を表している。よく見るとほとんどが小さな枝で終わっているのに、時々巨大な枝が形成され、それらの分布の仕方が冪乗則に従っているというわけだ。これほどきれいなモデルがあるだろうか。そしてこれと類似のことがこの世界で起きていると考えることができるわけだ。

冪乗則と揺らぎ ３

この説明からわかることは次のことだ。揺らぎとは、実はこのロングテールの長い尾で起きていることなのだ。何しろここが圧倒的に長いので、揺らぎはそれ自体が本体部分と見なされるが、実はとんでもない動きをする可能性を持っている。何しろ揺らぎは正確な正弦波や同じサイズのジグザグではない。それは時に大きく、時に小さくなり、突然とんでもない大きさの揺れを可能性として含む。ここで「可能性として」というのは、それは実はめったに起きないからだ。でも起きる時は起きる。そんなことが起きてもおかしくないことを予告するかのように、揺らぎは最初から不規則で、ある意味では思わせぶりで予想が不可能なのだ。ここら辺は、株価の動きに敏感な人は良くわかるだろう。

地震の話に戻って考えよう。地面は常に揺らいでいる。それはおそらく地殻のどこかで小さな岩がずれるということが起きているために起きる。つまりはプレート同士が少しずつズレながら動いている、という、ある意味では不安定な状況が生じているからだ。（地殻やプレートが全く動いていないのであれば、地震など起きようもない。）

さて小さな岩のずれはいたる所で起き、大抵はそれで収まってしまう。微震としてすら観測されないかもしれない。ただし稀に、近隣の別の不安定な岩に波及して、いわば連鎖反応を起こすことがある。これが起きるのはある意味ではすべての岩が同じように不安定だからだ。するとその二つの岩が動くことでその安定が治まることになるだろう。大抵の場合は。ところがそれが三つ目の岩を巻き込んだ少し大きな揺れで収まる場合も出てくる。そして稀に、それが四つ目の岩を巻き込んで少し大きな動きを起こすこともある。小さな地震と言ってもいい。すると・・・・、実に劇的なことが起きかねない。それは別の場所の同じような連鎖反応を起こしかねない。そんなことはめったに起きることはないが、起きる時は起きる。こうしてその極端な例が巨大地震となる。そしてその時に連動して動く岩のサイズと、その起きる頻度にはある重要な関係がある。つまり両方の対数を取ると逆比例しているのだ。これがグーテンベルグ・リヒター則というわけだ。

とまあなんとなくわかったような説明をしたが、実はこれでは本当に分かったことにならない。もう少し頑張ってみる。

先ず小さな岩が動く、という言い方をしたが、この「小さな岩」が曲者だ。その平均の大きさは?　おそらくそんなものはない。先ほどの天体の大きさと同じ議論により、岩の大きさに典型的なものはない。まあ「岩」と言えば数センチから数メートルくらいを言うだろうが、それはそのくらいの大きさの石を岩と呼んでいるからだ。この世界の鉱物をすべて集めて行列を作ったら、天体と同じようなロングテールを作るだろう。それを言い出したらどうしようもないので、ここは最小の単位を考えざるを得ない。そこで直径0.1ミリの砂粒を最小単位とする。岩石はそれが固く押し固められたものだ。そして最初に岩がずれて動いたというシーンをビデオに収めよう。そのビデオは時間を延ばしたり、対象を拡大したりすることが出来る。するとおそらくずれた岩と岩の間で起きていることにズームインすると、それは岩全体が突然動いたのではなく、最初はこぐ微小なずれによる破片の生成が、ズレた部分のどこかで起きていることがわかる。ズレが起きた数センチの部分をさらに拡大してみると、そのうちのごく一部がまず最初に動き出して、それが全体に波及したことがわかる。さらにその部分を拡大してみると・・・・。結局は最小単位である砂粒大のずれが起きていたことがわかる。そう、この最初の岩のずれは、ミクロのレベルで見れば大地震なのであった。もしそこに住んでいるアリがいて、その体験を語ってくれたら、「いえね、いつもちょっとした揺れなら起きているんですよ。でもあんな大きな揺れは久しぶりでした。ここで起きている揺れは大体ロングテールですからね。あんなのはめったにありません。」アリ君がどれだけ賢いかわからないが、一つ言えるのは、ほんの小さな岩の揺れは、彼らにとっては大地震だったということになる。

ここで少しまとめてみよう。ある状態においては、そこに存在する粒子が同じように不安定であるとする。すると最小の単位のずれ、ないし動きが連鎖反応を起こす可能性がある。そこではより大きな粒子に連鎖する可能性は急速に減っていくが、それでも起きることは起きる。その急速に稀になっていく仕方が、冪乗則に従うということだ。

冪乗則と揺らぎ ２

　実はこの冪乗則が実感としてつかめずに、私はここ10年くらい悩まされているのだ。ご存知の方もあろうが、これはフラクタルの問題と同等である。マンデルブローの幾何学図式は何処まで拡大していっても自己相似形が続いていく。つまりその図式のサイズを小さくしていけば、そこに含まれる相似形の数は無限大に向かっていく。その場合グーテンベルグ・リヒター則は完璧に成り立つわけだ。でも自然現象はマンデルブローの図形とは違う。それは地震の規模がある範囲においてのみフラクタル的な分布をするはずだ。それでも部分的にではあれ冪乗則に従うものは自然界にあふれているのだ。

私の愛読書の一冊に、「歴史は『べき乗則』でうごく」というのがあるが、英語の原題は“Ubiquitous” (遍在)である。つまりどこにも見られるというわけだ。自然のどこにもかしこにも見える冪法則。世界に遍在していて、それがようやくここ数十年で理解されるようになって来たのはどうしてだろう？
ここからしばらくは私の思考実験が延々と続くことをお許しいただきたい。

たとえばこんな感じだ。天体の大きさにはおそらく冪乗則が成り立つ。すると、この世に存在する天体を一列に並べて1,2,3・・・と番号を振る。あなたはその天体の一つ一つのサイズを測り、その平均値を取ろうとする。そこでそして順番に一つ一つ登場してもらう。最初はどのような計測装置が必要かわからなかったが、登場する天体がみな余りに小さく、目に見えないくらいなので、顕微鏡が必要になることがわかった。なぜなら天体の大多数は、目に見えないほどの宇宙のちりだ。いわゆる「宇宙塵」と呼ばれるものの大きさは、0.01マイクロメートルから10マイクロメートル程度であるとされる。すると土星のリングなどに含まれる塵などが数としては圧倒的に多く、それらの行列が延々と続くことになる。ところが時々、ごくたまに米粒大の天体が現れて、びっくりする。顕微鏡で見なくても、定規ではかれる大きさだ。そしてその作業を延々と、気の遠くなるほどの時間をかけて続けると、何年かに一度、それこそとんでもない大物が紛れ込む。数センチ、あるいは数十メートルというものも、ごくごくまれに登場する。そしてもっともっとごくまれに、とんでもない大物が出てくる。木星の衛星くらいになると、79個あるものの大きさは数キロ程度だという。しかしそのような大物が現れるのはごくごくまれで、また延々と塵が続いていく。あなたは気がついたらもう100年も計測を続けていて始めて、なんと月が登場する。そういえば月も宇宙の天体のひとつだ。ということは、地球も太陽も・・・・。しかし毎日塵レベルの測定に没頭されて、気がついたら数光年が過ぎて、ようやくある塵の次に地球サイズの天体が現れる・・・・。

ここでネットの力を借りたら、日本の天文学者がとんでもない巨大天体（「ヒミコ」）を発見したとある。ウィキ様に登場してもらう。

「ヒミコはハワイのすばる望遠鏡で大内正己によって発見された。発見された場所はすばるXMMニュートンディープサーベイフィールドであり、この範囲で他の207個の銀河候補とともに見つけられた。・・・データに基づけば、この天体は『早期宇宙で次の大規模な物体に比べ10倍以上の大きさで、太陽質量の400億倍の質量』を持ち、『大きさは5万5千光年でわれわれの銀河の半分くらいの直径』を持つとされている。なお、距離については巨大ブラックホールや銀河衝突の影響によって赤方偏移の数値が変わる可能性がある。ヒミコの発見によって、宇宙の初期に現代の平均的な銀河と同じ程度の大きさの巨大天体が存在したことになった。・・・・・」（ウィキペディア、「ヒミコ」）

「太陽の400億倍の質量」とサラッと言うけれどどうなのよ、と言いたい。そしてこの想像上の天体の列を考えると、冪乗則のニュアンスがつかめるのではないか？大きくなるにしたがって出現頻度はそれだけ少なくなる。大きさと頻度の両方の対数をグラフに描くと直線が得られる、とは実はそういうことだ。そして私たちの生活にこのような例はいくらでもある。いきなりトブが、私たちが有する所得について考えよう。人が持つ所得の行列を考える。するとおそらくほとんど一文無しの人の列が延々と続いて、たまに小金もちが並んでいる。かと思うとごくごくまれにそこそこのお金持ちがいる。そしてその額によってそのお金持ちのレア度が増していく。ごくごくごくまれに億万長者が混じっている。あるいはCDを売れ行き順に並べる。すると自費で出した売れないCDの列が延々と続き、時々ヒットが混じっている。そしてヒットの大きさと同時にレア度が増していく。

それらを暇な人が売り上げ順に並べると、以下のような表ができる。これがいわゆるロングテール（長い尾）の図式で、左端に行くほど天体の大きさ、所得の大きさ、CDの売れ行きは小さくなり、該当する天体、人、CDの数は莫大になる。他方右端はおそらくとんでもなく永遠に続いていく。

冪乗則と揺らぎ １

「冪（べき）乗則」の世界と揺らぎ

揺らぎとは実に不思議な現象だが、その背景の一つとしてとても大切な仕掛けがある。それが冪（べき）乗測 power law　と呼ばれるものだ。この世は冪乗則が支配しているといってもいいが、それが揺らぎの本質につながっているかどうかはわからない。しかし確実にその一つの原因としてかかわっていると考えるしかない。そこでしばらくはこの不思議な冪乗則の話になる。

揺らぎの基本的な例として、地面の動きを考えよう。極めて繊細な地震計を設置してその動きを観察する。以前は地震と言えば人が体感するものを指していたが、最近は「震度ゼロ」の地震、すなわち地震計にのみ感知され、体感はされない地震も含めている。そして分かったことは結局は微震も含めた地震は常に起きており、私たちが体験したり、災害を引き起こしたりする地震は、そのうちの例外的に大きいものなのだ、ということだ。「揺らぎ」という言葉を用いるならば、大地は常に「揺らいで」いるのであり、地震はそのうちの特に大きな揺らぎだということになる。ではいつ大きな揺らぎが起き、それがどの程度予測可能かということについては、実はよくわかっていないのだ。

　グーテンベルグ・リヒター則

こんな風に書くと地震とは予測不可能ででたらめな動きを示すような「揺らぎ」である、という感じがするだろう。ただし実はこの地震について、驚くべき事実がわかっているのだ。そしてそれがこの「冪乗則」ということと関係している。例えば皆さんにはこんなことが理解できるだろうか？

１．地震の大きさに「典型的なもの」ないし「平均の大きさ」はない。(あえて平均すると限りなくゼロになってしまう)

２．地震の大きさとその頻度は、それらを対数で表すと直線状に並ぶ。

つまり地震の大きさは実はでたらめではなく、極めて整然とした秩序とともに起きているということなのだ。

実はこのうち2の方は、いわゆる「グーテンベルグ・リヒター則 Gutenberg–Richter law」、つまり地震の発生頻度と規模の関係を表す法則として知られている。片対数グラフで表すと直線関係になるという関係があり、この世界では有名な発見であった。

この2の問題の意味を突き詰めると1もおのずと理解される。このグーテンベルグ・リヒター則を厳密に当てはめると、地震の規模が小さくなると、その頻度は膨大になっていく。つまりは「地震」の数で言えば、微震の頻度は膨大になり、逆に巨大な地震は極端に少なくなる。だから平均すると圧倒的に微震の方が数で勝ってしまい、結果として地震の大きさの平均は限りなくゼロに近くなるというわけだ。

デフォルトモードネットワークと揺らぎ ２

　実は私はこの問題をどう理解していいかについて、長いこと思案してきた。科学的な知見は沢山提出され、それぞれが自分たちの研究で得られた所見を明示する。それぞれの研究はエビデンスを提出しているのだ。しかしそれらは時には矛盾していたり、つじつまが合わなかったりする。それらのデータをどのように理解して、少なくとも治療的な仮説を作り上げるかは、実はそれぞれの臨床家にかかっているのである。という事で以下に示すのは私の独自の理解であるとお考えいただきたい。

私が特に注目するのは、いわゆるマインドフルネス瞑想に関する研究である。マインドフルネス瞑想においては、心がある一つのことに注意を向け続けることで、心がそこからフラフラと一人歩きをしていくことへのブレーキをかけるという事を継続的に続ける営みだ。
マインドフルネス瞑想でしばしば注意を向けるように促されるのが、自分自身の呼吸であり、たとえば鼻から唇にかけて息が吹きかけられるときの感覚などに焦点を向けることが要請される。人はそれをしばらくは行うことが出来るが、しばしばそれは中断される。気持ちはいつの間にかそこからそれて、他愛もない事柄に移っていく。それはある意味では必然的な事であり、心とは実は一定の事柄に注意を集中するという活動と、そこからフラフラ離れてしまうという活動を交互に行っているのである。これはたとえば何かを注視している際にも、時々瞬目して注視を再開するという運動に似ている。（実際瞬目時はDMNが生じているという研究もあるほどだ。Nakano et al. 2013）。
(Nakano, T, Kato, M, Morito, Y, Itoi, S and Kitazawa,S (2013) Blink-related momentary activation of the default mode network while viewing videos. PNAS 110: 702-706.)

　もしDMNが何らかの形で私たちの心的機能にとっての意味を持つとしたら（何しろ脳が使うエネルギーの75％を消費しているというのだから）TPN（課題遂行）はいずれはDMNに戻って行くという事になる。するとマインドフル瞑想が鍛えているのはこのDMNからTPNへのスイッチングという事になる。これは実は脳がDMNとTPNの間を本来揺らぐものであり、そのゆらぎの在り方をより心身にとってより良いものにするためのトレーニングという事にならないであろうか?　

デフォルトモードネットワークと揺らぎ １

デフォルトモード・ネットワークがつかめない人のために

　

　揺らぎとの関連でどうしても論じなくてはならないのが、いわゆるデフォルトモード・ネットワークの話だ。脳がいわばアイドリング状態、つまりボーっとしている時にも、実はしっかり活動していることが知られているが、その時に活発な活動を示すのが、脳の広範囲にわたる神経ネットワークであり、それがデフォルトモード・ネットワークと呼ばれるのだ。しかし脳トレや瞑想との関連で様々にこのデフォルトモード・ネットワークが論じられる割には、その正体がつかめない。私も脳科学者ではないので非専門家と言わざるを得ないが、おそらく脳の基本的なあり方を論じる際にどうしても深い意味を持っているとしか考えられないだけで、その正体はまだなぞが多い。

デフォルトモードネットワークdefault mode network はデフォルト状態で活動をしているネットワーク、という意味である（以下は省略してDMNと略記しよう）。話は脳波を発見したハンス・ベルガーに遡る。彼は人間の頭皮に電極を付けると、きわめて微小な電気活動が検出できることを発見した。そして1929年の論文で、「脳波を見る限りは、脳は何も活動を行っていない時にも忙しく活動しているのではないか」という示唆を行った。何しろ脳波を見る限り細かいギザギザが常に記録されているからだ。もしこれがフラットになってしまったら、それは脳が死んだことを意味するくらいである。しかし世の医学者たちは、たとえば癲癇の際に華々しい波形を示すことに注目したり、睡眠により顕著に変わっていく脳波の変化に注目する一方では、それ以外の時にも絶えずみられる細かい波のことは注意に止めなかった。ここで皆さんは雑音ないしはノイズについての議論を思い出すだろう。ノイズはそれが揺らぎとして抽出されるまでは、ごみ扱いされるという運命にあり、それは脳波でも同じだったのだ。

脳の雑音という以上の注意を向けられなかったDMNが注目を浴びるようになったのは、もちろんCTやMRIといった脳の活動を可視化する技術が用いられるようになったことと深いつながりがある。

そして実は何ら活動せずにぼんやりしている状態の脳で、かなり活発な活動が行われているという事が分かってきた。ここに示したのはDMNの際に活動している脳の部位を赤く示したものだが、これらは前頭葉内側部と後部帯状回と呼ばれる部位だ。これらの部位は脳が何もせずにアイドリング状態にある時に光るのであるが、何か注意を集中させている時には、これらとは別の部位が光るという事が分かり、脳の活動には大雑把にいって3つのパターンがあるのではないか、という事が分かってきた。それらはDMN以外にも、課題遂行ネットワーク（TPN）、そしてDMNとTPNの間をつなぐスイッチのような主要ネットワーク（SN）がありそうだ、という事が分かり、一気にこの議論は熱を帯びてくるようになった。

ところでネットなどでＤＭＮについて調べていくと、人は奇妙な体験をすることになる。それはDMNが脳にとって果たしていい働きをしているか、悪い働きをしているかという事がよくわからなくなってくるという事である。DMNは何も役に立っていないようでいて、脳の使うエネルギーの75％を使っているという事が言われ、脳がスムーズに活動を行う上で常に準備状態にしておくという重要な役割を果たすことを初期の発見者であるワシントン大学のマーカス・レイクルMarcus E.Raichle 博士が論じている。（Marcus E.Raichle, ME (2010) The Brains Dark Energy. SCIENTIFIC AMERICAN. (養老孟司, 加藤雅子, 笠井清登訳「脳を観る認知神経科学が明かす心の謎」の中で（日経サイエンス社、1997）

　DMNの特徴である、ぼんやりさせて心を浮遊させる、というと、まるで瞑想のように思えるが、実は瞑想はこのＤＭＮとは逆の活動なのだ、という記述にも出あう。最近流行しているいわゆるマインドフル瞑想などは、むしろ心を浮遊させないような試みといえる。つまり心をDMNに向かわせないことが心身の健康に役に立つ、という風に書いてある。しかし他方では、このDMNは人間が何か創造的な活動を行う上で決定的な役割を果たしているとの記載もされている。これはいったいどういう事だろうか?

いい加減さ 推敲 ４

ビブラートは揺らぎか？

ちなみに揺らぎと快楽についてのテーマを考えるとまず先に私の頭に浮かぶのが、ビブラートのことである。昔ブラスバンドでトランペットを担当した時、一級上の子安先輩が、実にすばらしい音色のトランペットを奏でていた。私は子安先輩のようにきれいな音を出せるにはどうしたらいいかを常に考えていた。すると彼の音は、他のブラスバンドの部員がだれもしなかったことをしていたことに気が付いた。それは彼がビブラートをかけていたという事である。単純な音の連続には決して表すことのできない表情を与えるビブラート。これはいったいなんだろう?　まさに音の揺らぎという事なのだが、音が揺らぐことの美しさを体で教わった体験だった。ちなみに私は子安先輩にビブラートがかかっているのはどうしてか、どうやっているのか、といろいろ聞いたことを覚えている。ところが子安先輩は頑なに「自分がそんなことをやっていない!」と否定するのである。しかし彼がよく練習の合間に歌謡曲やムード音楽を吹いている時には、それが美しく揺れているのは確かなのだ。しかし子安先輩は頑なにそれを否定する。私は自分でトランペットのビブラートをかける方法を見つけるしかなかった・・・・。

私はその頃ブラスバンドの中で指導に当たっていた音楽の先生に少しかわいがられていたのを覚えている。練習熱心だし、ちょっとはうまかったのだろう。子安先輩の弟分として見られるようにもなっていた。しかしその私がビブラートの練習をしているのを見て、苦々しい目でしか見られていなかったことも覚えている。確かにクラシックでは、弦楽器をのぞいてビブラートは普通は使わない。ブラスバンドではトランペットなどはパーン、という華やかな金属音を鳴らして貢献するわけで、確かにオーケストラのトランペットの演奏を聞いてもムード音楽で聞かせるようなビブラートのかかった音は聞けない。そのうちビブラートをかけるのは不良のやること、という意識が湧いてきた。子安先輩もそれで頑固に、ブラスパンドの演奏ではビブラートをかけられることを隠していたというところがある。

ちなみに天外伺朗氏は、そのシンセサイザーの研究から、電子楽器の音を、そのスピーカーの前で羽を回すとか、スピーカー自信を首振りさせるなどをすることにより、心地よく聞こえるようにするという事を早くから行っていたという。そこでそれを電子的に生み出そうとしたが、なかなかうまく行かなかったという体験を書いていらっしゃる。（天外伺朗、佐治晴夫　宇宙の揺らぎ・人生のフラクタル（PHPビジネスライブラリー、2000年）

つまりあまり機械的につくられた揺らぎはかえって美しさを損なうという事だろうか。歌唱法に関する書物などを読むと、ビブラートはそれが意識せずに、自然とかけられることに意味があるのだ、だから美しいのだ、という記述にも出あうが、その真偽は私にはわからない。

精神分析における揺らぎ ２

ひとつの例を挙げよう。ただしまったく架空の症例で、私が今作ったものだ。

Aさん（30歳代男性、としよう）は職場でいつも上司との間での確執を起こしてしまう。どうも直属の上司と言い争いをして、煙たがられ、結局職場にいられなくなるという事を何度か起こしている。Aさんはそれを上司からのパラハラと見なす傾向にあるが、これにはAさんの幼少時からの父親との確執が絡んでいることが想像される。その問題を考えたくてAさんは分析を受けることになったが、Aさんのその問題は分析家との関係の中でも少し形を変えたうえで繰り返されることになる。すなわちAさんは分析家（初老期の男性）に対しても敵愾心を向けるが、それは最初は理想化や迎合の混じった見えにくい形で表現され、それは治療関係の深まりとともにより見えやすい形で表現されるようになって行ったのである。分析家はそこに生じた転移関係についての解釈を加えていった。それによりAさんが無意識レベルで抱えていた父親への怒りが意識化され、それはAさんが分析家に対しても向けていたライバル心や怒りを明らかにすることにつながり、彼が分析家に対しても持ち始めていた敵愾心は形を変えていった・・・・。

ここに示された治療の展開はある意味では比較的典型的なものと言えるだろう。というか、そのように作ったのだ。そして分析家がAさんとの間で生じている転移関係をいかに明確にし、解釈の中でその姿を描き出していくかが治療にとってのかなめとなると考えるのが普通だ。ところが実際のAさんとの治療過程で、分析家はこの転移関係以外の様々なことを体験することになる。それは分析家がごく普通の感性を備え、また理論に捉われない素直な目を治療素材に向けていればおのずと見えてくるかもしれない。それは上に簡単にまとめた治療の進行の仕方とはかなり異なるものだった。

たとえばAさんと上司との間に繰り返されている問題。聞いているうちに分析家はこれまでAさんと関係していた上司達の態度に様々な自己愛的な問題を見るような気がする。それらの上司達もまたかつての彼らの上司との間に確執を抱えながらも、迎合することで上司に取り立てられることの方を望んだ。すると上司たちがAさんに対して行う様々なパワハラまがいの関わりには、彼らが上司達には飲みこんでいた鬱憤のはけ口というニュアンスもあり、Aさんはそれに屈することなく立ち向かっていたという側面もありそうだ。するとこれはAさんの父親との間に抱えていたエディプス的な問題と読めると同時に、Aさんが権威に安易に屈せず、自分の意志を貫いていたという側面も見えてくる。というよりこの両方の間を揺らいでいるという側面がある。

さて治療関係だ。Aさんの分析家への敵愾心は、実は分析家が持っていたAさんに対するライバル心、自分に反抗する息子に対する父親としての怒り、といった側面もどうしてもからんでくる。しかしここまで自分の気持ちを表現する患者をほかに体験したことがないため、分析家はAさんの中にある問題、そのためにこの社会で生きづらさを体験しているようなパーソナリティ傾向や、未処理のエディパルな問題も存在している気がする。つまりAさんと分析家との関係は転移関係とも、逆転移の行動化とも考えられる状況の間を動いているという事がわかる。

これでもかなり治療像は分かりにくくなっているが、この分析家がさらに上級の分析家からのスーパービジョンを受けると、また別の視点が加わってくる。Aさんが上司との間で対立を起こす際にしばしば見えてきたのが、上司とのある種の親密な関係がそれに先立っていたという事である。たいていAさんは上司に取り立てられ、かわいがられる。上司はAさんを部下として重用するが、それが一線を越えるとAさんにはある種の不安が生じるらしい。それからAさんの方から上司を突き放す態度が見られるようになり、それが上司の反発を買うことになる。そこにあるのはむしろAさんが持つ親密さへの畏れ、あるいはその背後にある同性愛的な衝動が関係しているようだ・・・・。

この最後のくだりは人間が他者と持つ関わりはきわめて多種多様で、さまざまな文脈を伴っているということを示そうとしたにすぎないが、分析的な治療とは、そのざまざまな捉え方が出来る治療関係に大胆に作図線を引いて一つの理解に落とし込むという行為に近いことがわかる。実際には混沌として予測不能な出来事をそのものとして把握しようとすると、ますます混乱を招き、それは来談者Aさんが望むところではない。そこで治療者はその中のどれかを選び取り、そこにフォーカスを当てていく。分析は揺らぐことを一時停止する。そしてしばらくは世界を定点観察し、また流動的な流れを一時的に固定して考えることにする。その際はとりあえずはAさんが両親との関係の中で抑圧していた感情を想定し、そこに焦点づけをし、治療方針を立てていく。それが精神分析的な手法である。