揺らぎ 推敲 49

揺らぎと「冪（べき）乗則」の世界

揺らぎとは実に複雑な現象だが、その背景にはあるとても大切な仕掛けがある。それが「べき乗則」と呼ばれるものだ。漢字では「冪乗則」である。英語では power law（力の法則）とシンプルだ。この世はこの冪乗則が支配しているといわれる。そしてこれまで考えてきた揺らぎの本質につながっているというのだ。そこで本章ではこの不思議な冪乗則（以下、「べき乗則」）の話になる。
ただしこの概念は極めて重要であるものの、少々厄介で分かりづらいかもしれない。不必要に感じられたらこの章は飛ばしていただいても差し支えない。

冪（べき）というのは見慣れない漢字だが、要するに10の何乗、という時の「乗」に相当する、同じ数字を何度も掛け合わせるという意味である。ある値が１，２，３，４と自然数で進行すると、それに対応する値がたとえば 2×2、２×2×２、2×2×2×２・・

・・という風にとんでもないスピードでどんどん進行していく、という意味である。ネズミ算式に増えていく、というあのニュアンスだ。

ここで揺らぎとべき乗則の関係を説明したい。そのために揺らぎの基本的な例として、再び地面の動きや地震を考えよう。地面は、自然界の中で揺らぎの性質を有する典型例だ。ふつう私たちは地震の時以外は地面は不動だと思いがちだ。しかし極めて繊細な地震計を設置してその動きを観察すると、地面はほとんど常に揺れ動いていることがわかる。

以前は地震と言えば人が体感するものを指していたが、最近は「震度ゼロ」の地震、すなわち地震計にのみ感知され、体験はされない地震も含めている。
そして分かったことは、結局は微震も含めた地震はかなり頻繁に起きており、私たちが体感できたり、災害を引き起こしたりする地震は、そのうちの例外的に大きいものなのだ、ということだ。「揺らぎ」という言葉を用いるならば、大地は常に揺らいでいるのであり、私たちが地震と呼ぶのはそのうちの特に大きな揺らぎだということになる。ではいつ大きな揺らぎが起き、それがどの程度予測可能かということについては、実はよくわかっていないのだ。

ところでこんな風に書くと、地震における「揺らぎ」とは予測不可能ででたらめな動きを示すのだ、という印象を与えるだけかもしれない。でも揺らぎは決してランダムで無意味、というわけではない。実はこの地震について、驚くべき事実がわかっているのだ。そしてそれがこの「べき乗則」ということと関係している。例えば皆さんにはこんなことが理解できるだろうか？

１．地震の大きさに「典型的なもの」ないし「平均の大きさ」は限りなくゼロに近づく。

２．地震の大きさとその頻度は、それらを対数で表すと直線状に並ぶ。

つまり地震の大きさは実はでたらめではなく、極めて整然とした秩序とともに起きているということなのだ。

この１．の「平均的な大きさがゼロに近づく」という事実はおそらくほとんどの人にとって理解に苦しむものではないだろうか。そしてここがランダム性との違いである。例えばサイコロをでたらめに振って出てくる数値を平均することはたやすい。1＋2＋3＋4＋5＋6を6で割って、21/6 = 3.5 というわけだ。ゼロになんかならないわけだ。

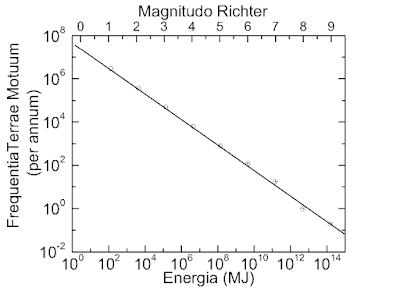
次に２．であるが、これはいわゆる「グーテンベルグ・リヒター則 Gutenberg–Richter law」として表されている。これは地震の発生頻度と規模の関係を表す法則である。片対数グラフで表すと両者は直線関係になるという関係があり、この世界では有名な発見であった。

この2. の問題の意味を突き詰めると1. もおのずと理解される。このグーテンベルグ・リヒター則を厳密に当てはめると、地震の規模が小さくなると、その頻度は膨大になっていく。つまりは「地震」の数で言えば、微震の頻度は膨大になり、理論上は震度ゼロの地震の頻度は無限大になってしまう。逆に巨大な地震は極端に少なくなる。だから平均すると圧倒的に微震の方が数で勝ってしまい、結果として地震の大きさの平均は限りなくゼロに近くなるというわけだ。

ちなみに数式で表すと、マグニチュードがM のときの地震の頻度をn（回/年）とすると、両者の関係は、パラメーター a 、b を使って次の式により表される。

{\displaystyle \log _{10}n=a-bM}log₁₀n = a-bM　または　n = 10^a-bM

ややこしい理屈は抜きにして、この式が表しているのは何かと言えば、マグニチュードが 1 大きくなるごとに地震の頻度は約10分の1になるということである。というよりはそのようにしてマグニチュードの値を定めたということだ。するとマグニチュードが1大きくなれば地震のエネルギーは約31.6倍ということになるのだ。